Probability with Martingales by David Williams

\[ \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\Z}{\mathbb Z} \newcommand{\N}{\mathbb N} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\abs}[1]{\lvert #1 \rvert} \newcommand{\Norm}[1]{\left \lVert #1 \right \rVert} \newcommand{\Abs}[1]{\left \lvert #1 \right \rvert} \newcommand{\pind}{\bot \!\!\! \bot} \newcommand{\probto}{\buildrel P\over \to} \newcommand{\vect}[1]{\boldsymbol #1} \DeclareMathOperator{\EE}{\mathbb E} \DeclareMathOperator{\PP}{\mathbb P} \DeclareMathOperator{\E}{E} \DeclareMathOperator{\dnorm}{\mathcal N} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\Var}{Var} \DeclareMathOperator{\Cov}{Cov} \DeclareMathOperator{\Leb}{Leb} \DeclareMathOperator{\Bin}{Bin} \newcommand{\wto}{\buildrel w\over \to} \]

Extra Gumption Exercises

The sample space is the unit square \([0,1]^2\) with points corresponding to \((x_1,x_2)\). The probability measure is the same as area in this square. A necessary and sufficient condition to form a triangle is that the segments \([0,x_1]\), \([x_1,x_2]\) and \([x_2,1]\) satisfy the triangle inequalities. Assuming \(x_1 < x_2\), these take the form

\[ \begin{equation} x_1 < (x_2-x_1) + (1-x_2) \qquad 1-x_2 < x_1 + (x_2-x_1) \qquad x_2-x_1 < (1-x_2)+x_1 \end{equation} \]

The first inequality says \(x_1 < \frac 1 2\), the second that \(x_2 > \frac 1 2\) and the last that \(x_2-x_1 < \frac 1 2\). These inequalities describe a triangle in the unit square with area \(\frac 1 8\). Considering also the symmetrical when \(x_1 > x_2\), the total probability is \(\frac 2 8\)

A spaceship \(X\) may communicate with any spaceship in the points in the hemisphere centered at \(X\). Denote this by \(h(X)\). Without loss of generality, rotate the sphere so that \(A\) is the north pole, and \(B\) lies in a fixed plane through \(O\) and \(A\). The three ships may communicate if:

• \(B\) is in the northern hemisphere and \(C\) is in the northern hemisphere (the ships can communicate via \(A\))

• \(B\) is in the northern hemisphere and \(C\) is in the half-lune \(h(B)\setminus h(A)\) (the ships can communicate via \(B\))

• \(B\) is in the southern hemisphere and \(C\) is in the half-lune \(h(A) \cap h(B)\) (the ships can communicate via \(C\))

These cases are disjoint, so we can consider them separately and sum their contributions. The area of a half lune is proportional to angle \(\angle XOY\) where \(X\) and \(Y\) are the centers of the hemispheres. This is the same as the dihedral angle between the equitorial planes of the hemispheres. Thus the probability of being in a half lune of angle \(\theta\) is \(\theta/2\pi\).

So writing one integral for each case above, conditioning on the angle \(\theta = \angle AOB\) and giving the probabity for \(C\) to be in the the configuration described by the case gives the equation

\[ \begin{equation} P = \int_0^{\pi/2} \frac 1 2 \,\, p(d\theta ) + \int_0^{\pi/2} \frac \theta {2\pi} \,\, p(d\theta) + \int_{\pi/2}^{\pi} \frac{(\pi-\theta)}{2 \pi}\,\, p(d\theta) \end{equation} \]

Now, the probability density of \(\theta =\angle AOB\) is given by \(\frac 1 2 \sin \theta \, d\theta\). Heuristically, this can be seen by consiering the infinitesimally thin strip on the surface of the sphere with constant latitue \(\theta\). This is like a cylinder (or frustrum of a cone) of side edge length \(r \,d\theta\) and radius \(r\sin\theta\), so the area is like \(2 \pi r^2 \sin \theta\, d\theta\). Normalizing by the total surface area \(4\pi r^2\) gives the probability density.

Calculating each contribution

\[ \begin{equation} \begin{split} \int_0^{\pi/2} \frac 1 2 \cdot \frac 1 2 \sin \theta \, d\theta &= \frac 1 4 \\ \int_0^{\pi/2} \frac \theta {2 \pi} \cdot \frac 1 2 \sin \theta \, d\theta &= \frac 1 {4\pi} \\ \int_{\pi/2}^{\pi} \frac{(\pi-\theta)}{2 \pi} \cdot \frac 1 2 \sin \theta \, d\theta &= \frac 1 {4 \pi} \\ \end{split} \end{equation} \]

Summing the contributions we find \(P = \frac{2+\pi}{4\pi}\)

Multiplying by random elements in \(\{a,a^{-1},b,b^{-1}\}\) is the same as taking a random walk on the Cayley graph of the free group with two generators (see figure). This is the rooted 4-regular tree. The depth of a vertex is the length of the unique path to the root, which is the vertex corresponding to 1 in the free group element. For any vertex of depth \(d>0\), there are three edges leading to a node of depth \(d+1\) and one edge leading to a node of depth \(d-1\).

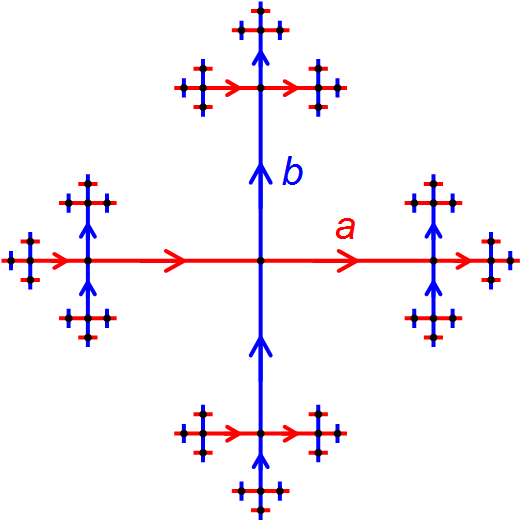Let \(p_d\) be the probability of returning to 1 starting from a node of depth \(d\). Its intuitively clear from the symmetry of the graph that the probability only depends on the depth. There is a graph isomorphism mapping any node of depth \(d\) to another node of depth \(d\), so there is a one-to-one correspondence between paths which lead back to 1, and those paths have equal probability. The probability must satisfy the recurrance

\[ \begin{equation} p_n = \frac 3 4 p_{n+1} + \frac 1 4 p_{n-1} \end{equation} \]

This is because we can condition the return probability on the first node in the walk and use the fact that the return probability depends only the depth of the node. Fundamental solutions of recurrance equations have the form \(p_n = \lambda^n\) and satisfy a characteristic polynomial equation which, for this recurrance is

\[ \begin{equation} 3 \lambda^2 - 4 \lambda + 1 =0 \qquad \Rightarrow \qquad \lambda = \frac 1 3 \text{ or } \lambda = 1 \end{equation} \]

The only solution of the form \(p_n = a \cdot {\frac 1 3 }^n + b\) which also satisfies the boundary conditions \(p_0=1\) and \(p_n\to 0\) as \(n\to \infty\) is \(p_n ={\frac 1 3 }^n\). In particular, a random walk starting at time 1 from a node of depth 1 returns to the origin with probability \(\frac 1 3\). This is the same as the event that the reduced word is ever 1 at positive time, since every word sequence as one letter at time 1.

Let \(L_n\) be the random variable which represents word length at time \(n\). Note that

\[ \begin{equation} \E[L_n \mid L_{n-1}] = \frac 3 4 (L_{n-1} + 1)+ \frac 1 4 (L_{n-1}-1) = L_{n-1} + \frac 1 2 \end{equation} \]

since \(L_n\) is the same thing as vertex depth. Taking expectations and using the tower law

\[ \begin{equation} \E L_n = \E L_{n-1} + \frac 1 2 \end{equation} \]

Hence the expectation satisfies a simple recurrance. Since \(L_0=0\), this means \(\E L_n = n/2\). More precisely, the quantity \(L_n-L_{n-1}\) is an i.i.d. random variable with finite variance and mean \(\frac 1 2\). Therefore by the SLLN, \(L_n/n\to \frac 1 2\) almost surely.

Contact

For comments or corrections please contact Ryan McCorvie at ryan@martingale.group